728x90
01. 프로베니우스 노름 Frobenius norm
- 모든 element 절대값을 제곱한 총합의 제곱근
X = np.array([[1, 2], [3, 4]])
# array([[1, 2],
# [3, 4]])
np.linalg.norm(X) # (1**2 + 2**2 + 3**2 + 4**2)**(1/2)
# 5.477225575051661
X_pt = torch.tensor([[1, 2], [3, 4.]])
torch.norm(X_pt)
# tensor(5.4772)
X_tf = tf.Variable([[1, 2], [3, 4.]])
tf.norm(X_tf)
# <tf.Tensor: shape=(), dtype=float32, numpy=5.477226>
02. 행렬곱 Matrix Multiplication
- 교환법칙이 성립하지 않음
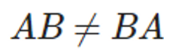
A = np.array([[3, 4], [5, 6], [7, 8]])
b = np.array([1, 2])
np.dot(A, b)
# array([11, 17, 23])
A_pt = torch.tensor([[3, 4], [5, 6], [7, 8]])
b_pt = torch.tensor([1, 2])
torch.matmul(A_pt, b_pt)
# tensor([11, 17, 23])
A_tf = tf.Variable([[3, 4], [5, 6], [7, 8]])
b_tf = tf.Variable([1, 2])
tf.linalg.matvec(A_tf, b_tf)
# <tf.Tensor: shape=(3,), dtype=int32, numpy=array([11, 17, 23], dtype=int32)>
728x90
'Study > Mathematics' 카테고리의 다른 글
| [선형대수학] 아핀 변환, 고유벡터, 고유값 분해 (0) | 2023.11.08 |
|---|---|
| [선형대수학] 역행렬, 대각행렬, 직교행렬 (1) | 2023.11.07 |
| [선형대수학] 아마다르 곱, 내각 (0) | 2023.09.05 |


