[ML] Multinomial Logistic Regression

01. Multi-class Classification

 

• label의 개수가 2개 이상인 경우 
  • ex. 학생이 어떤 전공을 선택할지 푸는 문제
  • ex. 혈액형이 무엇인지 맞히는 문제
  • ex. 뉴스기사가 어떤 카테고리인지 예측하는 문제
• 두 개 이상의 decision boundary 필요함
  • class가 k개인 경우 최소 k-1개의 classifier가 필요함
  • k개의 label에 대해서 k개의 서로 다른 class로 분류하는 decision boundary 사용(decision boundary는 서로에 대한 의존성 없이 특정 class에 대해서 효과적으로 분류하는 것이 목적)
  • 각각의 classifier를 서로 결합하여 어떤 class에 속하는 게 좋을지 최종 결정함

score vector에서 최대값을 가진 것이 label이 됨

 

 

 

 

 

02. Formulating Multinomial Logistic Regression

 

• 주어진 x와 학습하고자 하는 w가 결정되었을 때 이것이 j번째 class에 속하는지, 다른 class에 속하는지 확률을 계산함 

x : data, w : decision boundary

j번째 class에 속할 확률과 그렇지 않을 확률의 비율

• Sofrmax Function : Multi-class Classification 문제의 경우 각각의 데이터가 어떤 label에 속할지에 대한 확률을 표현함

normalization term을 통해서 총합이 1이 될 수 있도록 일반화

 

 

 

 

 

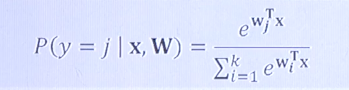
03. Formulating the Error Function

 

• binary classification을 k개의 label에 대해서 일반화한 형태
  • binary classification의 경우 cross entropy 형태로 error function 정의하여 y값이 1인 경우 최대, 0인 경우 최소가 되도록 확률값을 조정함
• multi-class classification의 경우 indicator function을 정의함
  • yi가 j번째 label에 속하면 1, 그렇지 않은 경우 0으로 표현
  • 그에 대응되는 확률값이 최대화되는 방향으로 w를 학습함
  • class 수가 3개 이상이므로 정규화 과정이 필요함 

 

 

 

 

 

04. Training Multinomial Logistic Regression

 

• 최적화 문제 solution
  1. closed form equation
     • 주어진 error function이 수학적으로 하나의 간결한 식으로 표현 가능한지 살펴보고 가능한 경우 방정식을 통해 최적의 해를 도출함(ex. linear regression model)
     • 단, 머신러닝 문제에서 이러한 closed form을 가지는 경우가 많지 않음
  2. numerical solution
     • analytic solution이 존재하지 않을 때 근사 해를 찾는 방식(ex. gradient descent method)
• multinomial logistic regression(=softmax regression)
  • logistic regression의 일반화된 형태 → closed form equation이 존재하지 않음
  • multinomial logistic regression 역시 gradient descent method를 이용하여 풀이함